
中学生の皆さんにとって、「偏差値」という言葉はよく見聞きすることでしょう。
しかし、「なんとなく知っている言葉だけど、詳しくは知らない」という方は、まだまだいらっしゃると思います。
偏差値とは、テストの点数や順位よりも客観的に、自分の学力を測定できる、信頼のおける指標です。
偏差値にについて、その実態を知っておくことには多くのメリットがあります。特に、受験を意識するなら非常に重要な数値です。
今回は、高校受験を控えた中学生の皆さんに向けて、偏差値とは何の数値なのか、受験においてどのように捉えるとよいのか、その活用方法について、ご紹介します。
偏差値とは何の数値なのか

偏差値とは、「集団内での相対的な立ち位置」を知る指標のこと。
皆さんの場合は、学力を測る指標として偏差値を使用します。したがって、「テストの点数を、特定の計算式によって変換した数値」のことだと思えばOKです。
偏差値50がスタート地点となり、平均よりテストの点数が良いと50以上に上昇します。反対に平均よりもテストの点数が低いと、50未満に低下していきます。これが偏差値です。
偏差値は学力を測定する方法として、広く使われています。なぜなら、「学力を客観的に数値化し、わかりやすく表わせる」という特徴があるためです。
ここからは、偏差値についてより踏み込んで解説していきます。
偏差値の考え方
こんなシチュエーションを思い浮かべてみてください。
テストAを1,500人で受け、あなたは75点をとりました。その後、テストBを3,000人で受け、あなたは65点をとりました。
この場合、二つの結果を比較できるでしょうか?
そう、順位や点数で単純に比べることはできませんよね。出題内容、実施された時期や平均点、参加人数も違うため、条件が合いません。
ここで、偏差値の出番です。
テストの点数や参加人数、平均点などを特定の式によって計算し、偏差値という指標に変換します。これによって、条件の違うテストであっても、共通の「ものさし」を使って比較できるようになります。
偏差値は、テストの参加人数や難易度、得点の幅といった、条件や結果の違いを計算式によって補正した値です。こうした要素の影響を受けづらく、安定した客観的な数値にできます。
したがって偏差値とは、テストの点を比較のために変換した、統計的な指標だといえるのです。
偏差値の計算方法
機会は多くありませんが、偏差値の式についてもここでご紹介します。
- 偏差値=(個人の得点−平均点)÷標準偏差×10+50
※ 標準偏差={(個人の点数 − 平均点)の二乗の総和 ÷ 受験者数}の平方根
上記に含まれる「標準偏差」とは、得点の散らばり具合を表す数値のこと。統計において、データのばらつき具合を考慮する補正のようなものです。
この計算式を、覚える必要はありません。模試などにおいては基本的に、偏差値はテストの結果とあわせて通知されるためです。
したがってこの計算式は、「偏差値というのは、きちんと根拠のある計算によって出された指標なんだな」という程度に、知っておいてもらえればと思います。
偏差値の見方
まず、真ん中が偏差値50であると知っておきましょう。
そのうえで、「偏差値50と比べて、どのくらい高いか・低いか」を確認することで、集団における自分の立ち位置を判定できます。
以下が、そのイメージです。
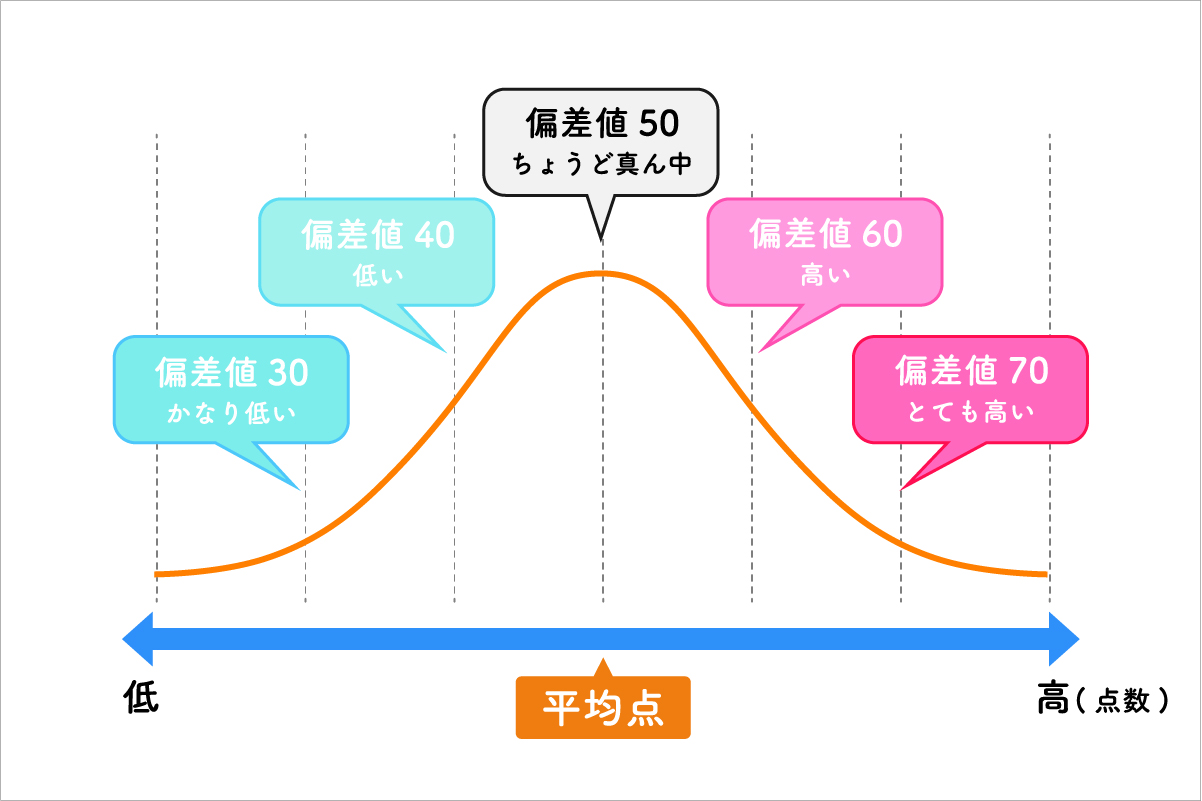
偏差値50に対して、
- 偏差値60は高い
- 偏差値70はとても高い
- 偏差値40は低い
- 偏差値30はかなり低い
- 偏差値50はちょうど真ん中
であるといえます。
もし、偏差値を用いてテストの結果を言い換えるのであれば、
- 偏差値60だったので、テストは「平均より上」という結果だった
- 偏差値70だったので、テストは「平均よりとても上」という結果だった
- 偏差値40だったので、テストは「平均より下」という結果だった
- 偏差値30だったので、テストは「平均よりかなり下」という結果だった
- 偏差値50だったので、テストは「ちょうど真ん中」という結果だった
と、いえるでしょう。
マラソンレースに例えて偏差値をイメージする
マラソンでは平均より速く走れる人ほど、順位が高くなりますよね。偏差値も同様、平均と比べて成績が良い人ほど、数値が高くなります。
レースの参加者全員の平均タイムを偏差値50とすると、平均より足が速い人は偏差値50以上、平均より足が遅い人は偏差値50未満ということになります。
そして、偏差値を知っておくことで、おおよその自分の順位を割り出すことが可能です。
例えば、偏差値70は「かなり高い方」であり、全体の上位2.3%に入る能力があるといえます。
具体的には、参加者が100人いたとすると、その中で上位2~3人に入るくらいの成績を出しているということです。
対して、偏差値30は「かなり低い方」であり、全体の下位2.3%に位置することになります。具体的には、100人中97位以下に該当する成績だと考えられます。これは、全体の中でかなり後ろに位置しているということです。
他にも、偏差値60は全体の上位16%に入る能力があることを意味し、順位としては大体上位1/6くらいの位置にいる……といった具合です。
このように、偏差値はマラソンの順位のように「他の人と比較して高いのか・低いのか」を知る指標になります。
偏差値は「汎用性の高いものさし」
偏差値は、一見すると、順位と似ているように感じますよね。
しかし、両者には決定的な違いがあります。それは、「集団の人数によって、順位の持つ意味が変動するかどうか」です。
例えば、受験者10,000人における200位と、受験者400人における200位では、順位の意味がまるで違いますよね。10,000人における200位は最上位グループですが、400人の中の200位は中間グループに位置します。
これに対して、偏差値55の持つ意味は、受験者が10,000人であっても400人であっても変わりません。
もちろん、母集団が極端に少ない場合はデータの偏りが大きくなるため、偏差値の信頼性が下がることもあります。しかしそれでも、偏差値は順位に比べて、汎用性が高い指標といえるでしょう。
テストの点と偏差値の違い
テストの点と偏差値についても、順位のときと同様に決定的な違いがあります。
それは「テストの点数は、テストの難易度によって簡単に上下する」という点です。
極めて簡単なテストであれば、80点、90点、100点を取ることも難しくないでしょう。反対に、ものすごく難しいテストの場合、得点が20点、30点となってしまうこともあり得ます。
このようにテストの点は、問題の難易度によって簡単に上下してしまうのです。
学校のテストで平均点が毎回大きく上下しないのは、先生方が上手にテストを作っているおかげ。本来、「テストで何点取れるか」というのは「問題次第」なのです。問題が簡単になれば点は上がりますし、問題が難しくなれば点は下がります。
余談ですが、筆者は高校時代、「先生が問題の難度を上げすぎたテスト」を受けたことがあります。現代国語のテストで、学年の平均点は30点台でした。先生は失敗を謝り、その先生が担当したテストに限って、学年全体で再テストが実施されたのを、今でも覚えています。
極端なエピソードかもしれませんが、こうした場合であっても、偏差値は通常通り機能するのです。偏差値は計算式に平均点を含んでおり、テストの難度によって大きくブレることがないよう、あらかじめ設計されています。
高校受験における偏差値の考え方

偏差値は、かなり正確に学力を表すとされています。そして、偏差値の高さは合格率に関係することは、広く知られています。
なぜなら、高校の一般入試は「成績順に、上から○○人目まで合格する」という仕組みで運用されているためです。
「合格ライン以上の点をとった人が全員合格」とはならず、定員という枠が決まっています。相対的な順位が下であれば、良い点数が取れたとしても、合格には至りません。これは怖いことですよね。
したがって受験においては、「集団の中での順位(相対的な立ち位置)」の方が、何点取れたかという「純粋なスコア」よりも重要なのです。
そして、多くの集団において相対的に良い立ち位置をキープし続けた受験生は、志望校の受験本番においても、これまでと同様に良い立ち位置にいやすい傾向にあります。
こうした背景から、受験における偏差値の重要度は高いのです。
偏差値を活用する方法

今後の学習への利用や志望校選びなど、偏差値はさまざまなシーンで活躍します。
自分の成績の「立ち位置」を把握する
偏差値によって、志望校に合格するためにあとどのくらいの学力が必要なのか、あるいはすでに合格に十分な学力がついているのかといった、受験における自分の立ち位置を測ることができます。
例えば、今の偏差値が50、志望校の偏差値が57だとします。この結果からは、「合格ラインに到達するために、偏差値を7アップさせる必要がある」と読み取れますよね。
先述したように偏差値とは、別々のテストを比較できるようになる「汎用性の高いものさし」です。したがって、「現在のテストの偏差値」と、「志望校の偏差値」であっても比較できるわけですね。
このように、偏差値をもとに受験本番の成績を予測することで、この先の受験対策に役立てることができます。
自分の得意・不得意を把握する
偏差値によって、自分の得意・不得意を把握し、受験本番までの時間を効率的に使うことができます。
例えば、通算偏差値が60を超えていても、いくつかの教科の偏差値が、60を下回っている場合があります。これは平均以上ですが、あくまで「得意教科で苦手教科を補っている」状態です。
60点を80点にアップさせるのは、80点を90点にアップさせるよりも、ずっと簡単です。これは偏差値に置いても同じことがいえます。ハイレベルな集団の中で抜きんでるよりも、平均的な集団に追いつく方が、ずっと簡単なのです。そのため、偏差値が低い教化から手を付けたほうが、コストパフォーマンスが良くなります。
偏差値で成績を見ることによって「合格に向かって効率的に成績をアップさせるには、どこから手を付けるとよいのか?」がわかったわけですね。
加えて、目標を立てる際にも偏差値は有効です。テストの点は難易度によって上下しやすいため、偏差値を目標にしたほうが、より客観的に勉強の成果を判定できます。
したがって、テストの得点そのものを目的とするのではなく、「国語の偏差値を51まで上げよう」という目標のほうが、より実践的といえるでしょう。
このように偏差値を活用することで、自分の得意・不得意をより客観的な数値で把握し、効率的な受験勉強に役立てることができます。
偏差値が極端に下がった場合は要チェック
偏差値に極端な上下があった場合、その原因を見直すことで苦手な分野が見えるケースもあります。
例えば、急に偏差値が下がったとき「もしかして、自分にとって苦手な分野からの出題が多かったのでは?」と疑ってみましょう。ここには、「平均的な集団は、この問題が解けた。しかし、自分には解けなかったため、偏差値が極端に下がった」という背景が隠れていることがあります。
このように、自分の得意・不得意を把握することにも、偏差値は活用できます。
志望校選びの参考にする
自分と高校の偏差値を見比べることで、志望校選びの参考にすることが可能です。
志望校を選ぶ際は、自分の偏差値から上下3から5の範囲にある学校を選ぶことが、セオリーとされています。偏差値が55であれば、偏差値が50から60の高校に出願する。これが受験における定石です。
この範囲であれば、入学後に「授業が難しすぎてついていけない」となることも少なく、適した進学先であるといえます。
受験における出願というのは、そう何度も経験することではありません。これは、生徒の皆さんだけでなく、保護者の方であっても同様です。
こうした状況下で、数字による根拠を参考に受験先を判断できるのは、非常に心強く感じるでしょう。あくまで参考に留まりますが、志望校選びにおいても、偏差値は信頼性の高い指標だといえます。
自分の偏差値を知る手段

自分の偏差値を知る最もシンプルな方法は、模試の受験です。特に、全国模試や全県模試など、大型の模試がよいでしょう。
なぜなら偏差値は、実際に競合する集団に近い環境で測定するほうが、データの信頼性が高くなるためです。
反対に、ローカルな範囲で実施される学校の定期テストの偏差値というのは、受験における意味が薄いといえます。実際に競合する集団を、十分カバーしているとは言い難いためです。
ただし、小規模であっても、自分の志望校に特化した模試が実施されている場合は、受験した方がよいでしょう。これは、模試の受験者と実際の競合先が似ており、信頼性の高い偏差値を得られるためです。
加えて、模試においては教科別に偏差値を知ることができ、自分の学力をより正確に測れるというメリットもあります。また、各問題の正答率など、さまざまな情報を得ることが可能です。
偏差値に限らず、模試には多くのメリットがあります。そして、受験勉強というのは自分の実力を数字で把握することからすべてが始まります。
まだ模試を受けたことがない方は、ぜひ一度、申し込んでみてください。
まとめ
偏差値とは、「特定の計算式によって、テストの点数を共通のものさしに変換した数値」のこと。「全体の平均に対して、自分の成績はどの程度の立ち位置にいるのか?」に応えてくれる指標です。
平均点や問題の難易度の影響を受けにくく、条件が異なるテストでも学力を比較しやすいといった特徴があります。
受験においては、学力の数値化という面で、偏差値は大きな意味を持ちます。自分の学力を知り、志望校の合格に向けてあとどのくらいの勉強が必要かが数値化できます。また、志望校を選ぶ際にも、参考の一つとして頼りになります。
もし、より信頼性のある偏差値を知りたい場合は、模試を申し込むところからスタートしましょう。特に、全国模試や、それぞれの都道府県で行われる大規模な模試であれば、さらに信頼性の高い偏差値が得られます。
今回は、「偏差値とは?」という疑問にお応えしながら、受験における偏差値や、その活用方法についてご紹介しました。塾や学校、もしくはおうちの中で偏差値が話題になった際には、ぜひとも思い出していただけたらと思います。




